Priority Queues in Theory
The idea behind a priority queue is simple. It mostly acts like a standard queue, where items are put into the queue, and then items are taken out of the queue. The difference comes from which items are taken out of the queue first. In a standard queue, the first item put in will be the first item taken out. This type of queue is also referred to as a FIFO or First-In First-Out queue, as opposed to a LIFO, or Last-In First-Out queue, also known as a stack. In a priority queue, each item is assigned a key value, and the item with the lowest (or highest) key value is taken out of the queue first, regardless of the order that the items were put into the queue.
The key values can be anything useful for maintaining the priority queue. In our case it was advantageous for Dijkstra's algorithm to use a key value that was some heuristic of how close the game was to an empty board. That way the next closest move to the end-of-game condition could be taken from the queue and checked. If we can pull the next closest move out of the queue faster than we can search all of the moves up to that move, then we will easily win out over BFS.
The trick is to structure the priority queue in a way that makes it fast to extract the item with the minimum key value. We can't go searching through the entire queue for the minimum each time because we're letting the queue grow to 250,000 items. It would take way too long to search through such a big queue every time through the search loop, looking for the minimum key value. Similarly, it would take too long to keep the array sorted as new items were inserted because inserting items in the middle of the array would require shifting all of the items after the inserted item, taking linear time with the number of items in the queue.
Another option is to use a Binary Search Tree (BST), where each node has a left and a right child, and all children to the left of a node will have keys that are less than that node, and all children to the right of a node will have keys greater than that node. A BST can be searched and nodes can be inserted in O(lg n) time, but because we're continually removing the minimum node, the tree can easily become unbalanced. Operations on an unbalanced BST have worse running times. This issue could be alleviated by using a special BST, like a red-black tree, that maintains a balanced structure, but we would still need to deal with the added size of a more complex data structure. Red-black trees have a fair amount of overhead compared to an array, and that would mean less room in memory for the 250,000+ moves we want to keep in the priority queue.
Numerous other options exist for priority queue data structures, but one of the most elegant and simple structures that has everything we need is the binary heap. It can be implemented cleanly using an array, so it doesn't have much overhead, and the operations for inserting items and extracting the minimum key value have the desired O(lg n) running time. That means pulling out the next move from a queue of 250,000 moves will only take about 18 times longer than a queue of 1 move, instead of 250,000 times longer if extracting the minimum had a linear running time of O(n). The JavaScript priority queue that we used when implementing Dijkstra's algorithm implements the binary heap as one of its choices of data structures behind the priority queue. Let's take a deeper look at how this data structure works.
Binary Heap Insertion (Enqueue)
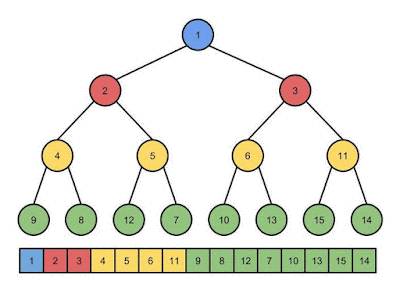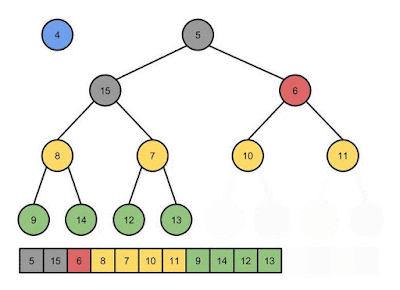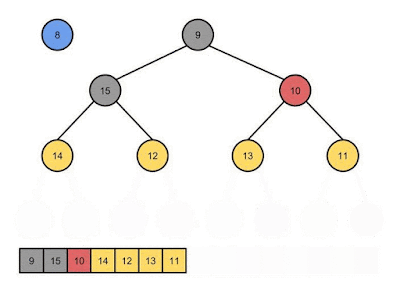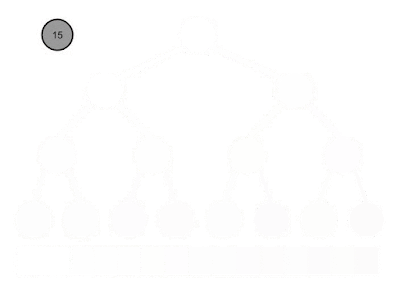
While the binary heap is implemented on top of an array, adding a specific way of managing the array elements and a couple new operations to the normal array operations, it is easier to think of it as a binary tree (but not a binary search tree, that's different). The tree is filled from left to right on each level of the tree before advancing to the next level and filling from left to right again. This method of filling the tree allows for easy storage in an array because new items can be added to the array by simply incrementing the index. The following picture shows the correspondence between the array behind the heap and the tree with nodes labeled by their index in the array.
The tree is a heap when it maintains a specific property among all of its nodes. The key value for each node is the minimum key value among all nodes in its sub-tree. The above picture also satisfies this heap property if we assume that the numbers in the nodes are key values. We'll see shortly how this property can be maintained during insertion operations, but look at what we get with it. By definition, the minimum key value is at the root of the tree, which means it is the first element in the array, so we can always find it immediately.
In order to implement insertion, we'll need to be able to quickly find the parent of a node. Due to how the heap is stored in the array, the parent of a node is simply the node's index divided by two. But arrays are zero-indexed, so we need to adjust slightly for that, giving us the following formula for finding a node's parent:
parent = (node - 1) / 2
Now, when inserting a node, we can stick it at the end of the array, and keep comparing it with its parent. If the node is less than its parent, swap them and compare the node with its new parent. We are guaranteed to maintain the heap property for every parent that's swapped because that parent was less than its other child before the swap, and we're replacing it with a node that's less than the parent after the swap. Therefore, the new parent is less than both of its children. The code is straightforward:
function BinaryHeap() {
this.data = [];
}
BinaryHeap.prototype.enqueue(value) {
this.data.push(value);
var i = this.data.length - 1;
while (i > 0) {
var parent = (i - 1) >>> 1;
if (this.data[i].key < this.data[parent].key) {
var x = this.data[parent];
this.data[parent] = this.data[i];
this.data[i] = x;
i = parent;
} else {
break;
}
}
}Notice that a node inserted into the binary heap will start at a leaf node and at most swap with all of its parents on its way up to the root node, if it happens to have the smallest key in the heap. Since the heap is a full binary tree except for the last, possibly partial, level and the height of a full binary tree with n nodes is lg n, the running time of this function is O(lg n).
That's basically all there is to inserting into a binary heap. This gif shows what happens when building up a heap by inserting somewhat random elements:
Binary Heap Extraction (Dequeue)
Extracting the minimum key value from the heap is a two step process. First, we need to find the minimum key, which is easy because it's the root of the heap and the root is the first item in the array. Second, we need to fill in the root with the new minimum key value in the heap. This step is a little trickier, but still not too bad.
To fill in the root, the easiest item to use is the one at the end of the array. We can take that item and put it in for the root, reducing the size of the array by one in the process. Now we most likely don't have the minimum key at the root, so we have to fix that. We can fix the heap by comparing the root with both of its children and swapping it with the child with the smaller key. This swap will restore the heap property between the root and its children because it now has the smallest key of the three nodes.
The entire sub-tree of the child that was not swapped also still satisfies the heap property because it hasn't changed from before the operation, except possibly by removing one of its leaves if the last item in the array came from its sub-tree. The sub-tree with the swapped child will need to be fixed, so we can repeat the same comparison and swap with it and its children as was done with the root. We can continue moving the leaf node that came from the end of the array down the heap until it's key is less than both of its children. At that point the heap property has been fully restored, and the extraction is complete. The code reflects this description quite closely:
BinaryHeap.prototype.dequeue() {
if (this.data.length === 0) {
throw 'Empty queue';
}
var min = this.data[0];
var last = this.data.pop();
if (this.data.length > 0) {
this.data[0] = last;
var pos = 0;
var last_idx = this.data.length - 1;
while (true) {
var left = (pos << 1) + 1;
var right = left + 1;
var min_idx = pos;
if (left <= last_idx &&
this.data[left].key < this.data[min_idx].key) {
min_idx = left;
}
if (right <= last_idx &&
this.data[right].key < this.data[min_idx].key) {
min_idx = right;
}
if (min_idx !== pos) {
var x = this.data[min_idx];
this.data[min_idx] = this.data[pos];
this.data[pos] = x;
pos = min_idx;
} else {
break;
}
}
}
return min;
}left_child = node*2
right_child = node*2 + 1
You can check the picture of the binary heap and its corresponding array to convince yourself that this is true:
Since the real code has the array index starting at zero, we need to add one to the left child index to get the right index. After that, we assume the current node has the minimum key, compare it to both of its children, and if the minimum key has changed after the comparisons, we swap the current node with the node with the minimum key. Otherwise, we're done and we can return the original minimum node that we had saved off before fixing the heap.
It is easy to see that this function runs in O(lg n) time for the same reason that insertion did, except the node is moving down instead of up the tree. The new root will at most travel down from the root to a leaf node, and the height of the tree is lg n for n nodes. Take a look at what it looks like for items to be extracted from the binary heap:
That's about all there is to a binary heap. It's a neat little data structure that elegantly solves the problem of implementing a priority queue. It has the nice property of using an array for efficient storage of items in the queue, and the heap property can easily be maintained with efficient insert and extract operations. It's a great data structure to have in your tool set.
We've just about wrapped up our exploration of simple game algorithms with Color Walk. We've covered a lot of ground through all of these posts, so next time I'll do a summary of all of the strategies we've looked at and how far we've come in solving this simple game.
Article Index
Part 1: Introduction & Setup
Part 2: Tooling & Round-Robin
Part 3: Random & Skipping
Part 4: The Greedy Algorithm
Part 5: Greedy Look Ahead
Part 6: Heuristics & Hybrids
Part 7: Breadth-First Search
Part 8: Depth-First Search
Part 9: Dijkstra's Algorithm
Part 10: Dijkstra's Hybrids
Part 11: Priority Queues
Part 12: Summary